关于树的知识

首先，数据结构分为逻辑结构和存储结构，这里我们也要把树的逻辑结构和存储结构分开来讲。

树的最基本的定义：
树是n（n>=0）个结点的有限集合。当n==0时，称为空树；任意一棵非空树满足以下两个条件：

1. 有且只有一个特定的称为根（root）的结点；
2. 当n>1时，除根结点之外的其余结点被分成m(m>0)个互不相交的有限集合T1,T2,…,Tm，其中每个集合又是一棵树，并称为这个根结点的子树（Subtree）。

显然，树的定义是递归的。

其它所有的树都是在树的基本定义的基础上添加限制条件而得到的，他们都具有不同的特点，也因此有不同的用途；

树的表示形式：

1. 树形图
2. 嵌套图
3. 凹凸表
4. 广义表

树的几种基本存储方法：

1. 双亲表示法
2. 孩子表示法
3. 双亲孩子表示法
4. 孩子兄弟表示法

二叉树：

1. 二叉树区分左子树、右子树，但是左右不分大小

二叉排序树：
它或者是一个空树，或者是具有如下性质的二叉树：

1. 如果它的左子树不为空，则它的左子树的所有结点的值均小于其根结点的值
2. 如果它的右子树不为空，则它的左子树的所有结点的值均大于其根结点的值
3. 它的左右子树也分别为二叉排序树

用途： 二叉排序树的中序遍历是一个有序序列

二叉搜索树（也叫二叉查找树）：
很多地方把二叉搜索树与二叉排序树当成一个概念； 我觉得二叉搜索树应该是一个平衡二叉树，因为只有平衡才能保证搜索的最大时间复杂度为O(logⁿ);
对于二叉排序树，在极端情况下（如斜树），查找的最坏的时间复杂度为O(n);

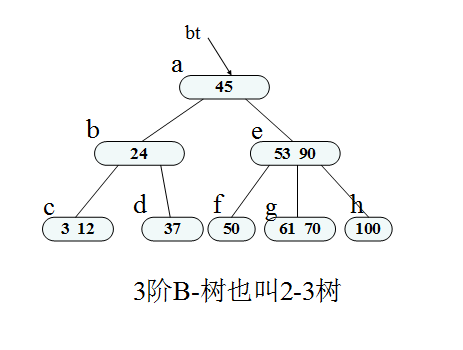
B-树：
B-树是一种平衡的多路查找树； 一棵m阶的B-树或为空树，或为满足下列特性的m叉树：

1. 树中每个节点至多有m棵子树
2. 若根结点不是叶子结点，则至少有两棵子树
3. 除根结点之外的所有非终端结点至少有[m/2]棵子树
4. 所有的非终端结点中包含下列信息数据(n,A0,K1,A1,K2,A2,…,Kn,An)其中Ki(i=1,…,n)为关键字，且Ki<Ki+1,(i=1,…,n-1); Ai(i=0,…,n)为指向子树根节点的指针，且指针Ai-1所指子树中所有节点的关键字均小于Ki(i=1,…,n),An所指子树中所有节点的关键字均大于Kn,n([m/2]-1)≤n≤m-1)为关键字的个数（或n+1为子树个数）。
5. 所有的叶子结点都出现在同一层次上，并且不带信息（空指针）。

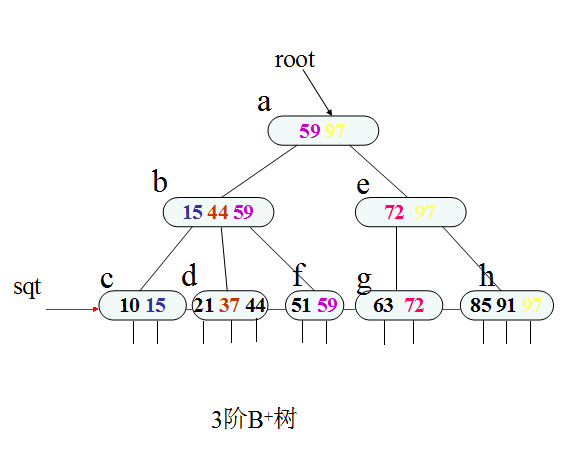
B+ 树：
B+树是B-树的变型，m阶的B+树和m阶的B-树的区别是：

1. 关键字个数和子树个数一样多
2. 所有叶子结点中包含全部关键字信息及指向含这些关键字记录的指针，且叶子节点本身依关键字的大小自小而大顺序链接。
3. 所有非终端结点可看成索引，节点中仅含有其子树中的最大（或最小）关键字

键树：
键树（数字查找树）：是一棵度≥2的树，树中每个结点不是包含一个或几个关键字，而是只含有组成关键字的符号。如数值中的每一位，单词中的每个字母。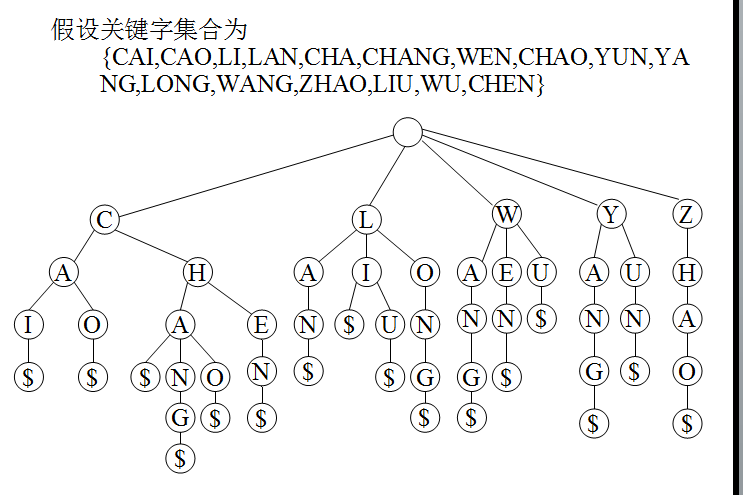

还需要了解的：
    红黑树、AVL(平衡二叉树）、Treap、伸展树 等。

本次学习从百度百科、百度文库中学到不少东西。

参考资料：
http://baike.baidu.com/view/593144.htm